Enthalpy, Entropy, 2nd Law, and 3rd Law

Enthalpy, H, is the heat contenet of a system. Enthalpy can always be calculate by,

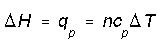
The change in enthalpy is reference to be the heat transfer at constant pressure. We can calculate enthalpy change this way for any system because enthalpy is a state function. More generally enthalpy change calculated in terms of internal energy change and a pressure-volume correction,

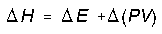
and setting PV = nRT we get,

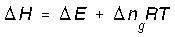
Where delta n_g is the change in moles of gas (final - initial).

Entropy, S, is a state function and is a measure of disorder or randomness. A positive (+) entropy change means an increase in disorder. The universe tends toward increased entropy. All spontaneous change occurs with an increase in entropy of the universe.

The sum of the entropy change for the system and the surrounding must be positive(+) for a spontaneous process.

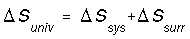
Lets calculated entropy changes for different type of processes.

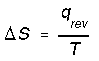
*Reversible gain/loss of heat at constant T (reversible isothermal).

*Phase transitions such as fusion and vaporization. e.g. entropy change for vaporization would be,

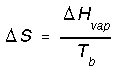
Most liquids have nearly the same molar entropy of vaporization. Trouton's rule estimates that it is 83-93 J mol^-1K^-1. For freezing we calculate entropy change in a similar way except we use the heat of fustion and the freezing temperature.

*Reversible heating/cooling at constant V (reversible isochoric). When a system cools, its entropy decreases. The entropy change is negative (-) with a decrease in temperature and positive (+) with an increase in temperature. We calculate isochoric entropy change by,

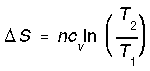
*Reversible heating/cooling at constant P (reversible isobaric). We calculate entropy change for isobaric processes in a similar way to isochoric processes.

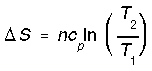
*Reversible expansion/compression at constant T(isothermal). The entropy of the system increases with its size according to,

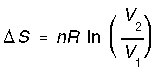
and since P is inversely related to V,

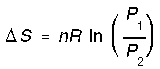
All these formulas assume ideal behavior.

Reversibility is an ideal concept. In genergal most real world processes are irreversible. The work and the heat transfer (because they are path dependent) will differ between reversible and irreversible processes. The following summarizes the differences:

_irrev

_rev

-w_irrev < -w_rev

The work done by the system irreversibly is less than work done by the system reversibly.

The Second Law states that

*In a reversible process the total entropy of a system plus its surrounding is unchanged. delta S_univ = 0.
*In a irreversible process the total entropy of a system plus its surrounding increase. delta S_univ > 0.

*The universe tends toward disorder or randomness. delta S cannot be less than 0.

The following is a list of things that increase or decrease entropy. 1) Gases have higher entropy than liquids, and liquids higher than solids.

2) Low pressures have higher entropy than high pressures.

3) Dilute solutions have higher entropy than concentrated solutions.

4) Dissolved substance have higher entropy then its undissolved form.

5) Entropy increases with increasing temperature.

The Third Law sets the zero of entropy for a pure perfect crystal of a substance at 0 K. We can then reference this zero of entropy can calculate standard state entropy changes. Some of these values are listed in Appendix D of Oxtoby. We calculate the standard state entropy changes as we did with standard state enthalpy changes.