Neuhauser Group

UCLA Department of Chemistry and Biochemistry

• Home
• Research
• People
• Publications
• Comp.Chem.
• Class Notes
• Contact
• StochasticGW

Selected recent publications

A GW approach that gives accurate charging energies for very large molecules and clusters (thousands of electrons and more, scaling linearly with system size due to the use of stochastic algorithms) [PDF]

A linear-scaling embedded-fragment stochastic approach to the densities and energies of large molecules (thousands of electrons or more). The method is non-approximate, and its new, embedded-fragment version uses very few stochastic orbitals (tens to few hundred orbitals regarless of system size) since the stochastic averaging only needs to model the small difference between the true (unbknown) density and the sum of fragment densities. [PDF]

Stochastic GW

We have recently developed a formalism to calculate quasiparticle energies within the GW approximation using stochastic orbitals. The GW approximation offeres a highly accurate theory for calculatiing quasiparticle energies in a semiconducting materials. Practical use, however, is limited by the theoretical fourth-order scaling with respect to system size.

We have recently developed a stochastic, orbital-free formalism which effectively circumvents the issues with scaling. In our method, the occupied and virtual orbitals of the Kohn-Sham Hamiltonian are replaced by stochastic orbitals used to evaluate the Green function G, the polarization potential W, and thereby the GW self-energy. The method enables linear scaling calculations, breaking the theoretical scaling limit.

We illustrated the utility of the method for silicon nanoclusters of various sizes, the largest of which have over 3000 electrons, and various organic fullerenes.

Stochastic DFT

In the standard implementation of Kohn-Sham DFT, the electron density is

\(\rho(r) = 2[|\psi_1(r)|^2+|\psi_2(r)|^2+\ldots+|\psi_{\text{HOMO}}(r)|^2 \)
The occupied states are in turn obtained by diagonalzing the density-dependent Kohn-Sham matrix. Formally, matrix diagonalization scales as N³. In stochastic DFT, on the other hand, the electron density is obtained as the average over densities of filtered stochastic orbitals:
\(\rho(r) = <|\xi_{filtered}(r)|^2>_{\xi}\)
The number of stochastic orbitals required is typically independent of the number of electrons resulting in an overall linear or sometimes sublinear scaling with this method. We also have developed embedded fragment and overlapped embedded fragment stochastic DFT which allows us to study covalently bonded systems more accurately.

Stochastic TDDFT

In conventional Kohn-SHam TDDFT, all occupied orbitals will be propagated individually. This makes TDDFT expensive for larger systems. In stochastic TDDFT, instead of propagating all occupied orbitals, we instead propagate the filtered stochastic orbitals. Each such orbital is a linear combination of all occupied states and thus carries the information of the entire system.

Correlation Energies

Local and semi-local corrlation functionals commonly used within DFT fail to describe long-range van der Waals interactions and other types of dynamical screening effects. Post-DFT corrections to the correlation energy, such as MP2 and RPA, offer a straightforward method for improving estimates of various observables. The main hurdle with higher-order correlation energies is computational complexity. Similar to the research above, we can use stochastic orbitals to replace large sums over occuopied and virtual KS orbitals.

Density functional theory

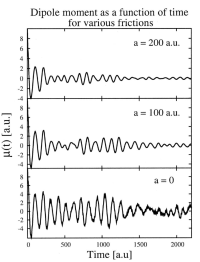
We also develop and implement improved time-dependent density functional theory (TDDFT) approaches suitable for nanoscale device modeling. These include:

• Orbital-free DFT methods
• Hydrodynamic tensor DFT
• Quantum Drude friction